Miért fontos a statisztikai szignifikancia?
Fedezze fel, miért számít a statisztikai szignifikancia az adatelemzésben, a kutatásban és az üzleti döntésekben. Ismerje meg a p-értékeket, a hipotézisvizsgála...
Ismerje meg, hogy a statisztikai szignifikancia hogyan határozza meg, hogy az eredmények valósak vagy véletlenszerűek. Értse meg a p-értékeket, a hipotézisvizsgálatot és a gyakorlati alkalmazásokat vállalkozása számára 2025-ben.
A statisztikai szignifikanciát arra használják, hogy meghatározzák, egy eredmény véletlenül vagy valamilyen vizsgált tényező miatt következett be. Ha statisztikailag szignifikáns, akkor valószínűtlen, hogy pusztán a véletlen okozta.
A statisztikai szignifikancia alapvető fogalom az adatelemzésben, amely segít megkülönböztetni a valódi hatásokat az adatok véletlenszerű ingadozásaitól. Amikor kísérleteket, felméréseket végez, vagy üzleti mutatókat elemez, megbízható módszerre van szüksége annak eldöntéséhez, hogy a megfigyelt minták valósak vagy csak a véletlen eredményei. A statisztikai szignifikancia ezt a kritikus keretrendszert biztosítja matematikai elveken keresztül, értékelve annak valószínűségét, hogy a megfigyelt eredmények akkor is előfordulnának, ha valójában nem lenne hatás vagy különbség az összehasonlított csoportok között.
A fogalom Ronald Fisher statisztikus munkásságából származik a 20. század elejéről, és azóta a hipotézisvizsgálat sarokköve lett szinte minden, adatelemzésre támaszkodó területen. A gyógyszerkutatástól, amely új kezelések hatékonyságát igazolja, az e-kereskedelmi cégekig, amelyek konverziós arányokat optimalizálnak, a statisztikai szignifikancia választja el a valódi felismeréseket a félrevezető következtetésektől. A statisztikai szignifikancia működésének megértésével megalapozott döntéseket hozhat, amelyek mögött valódi bizonyíték áll, nem csupán intuíció vagy véletlen.
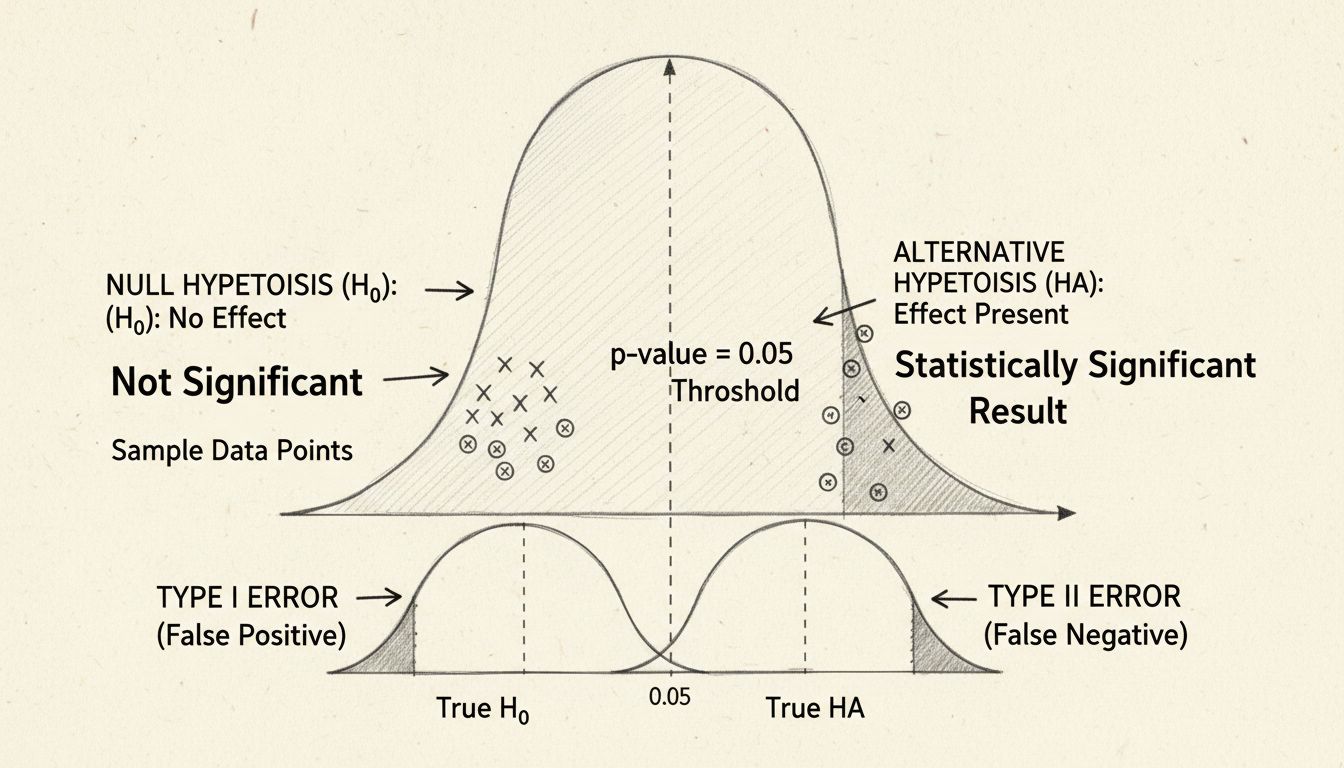
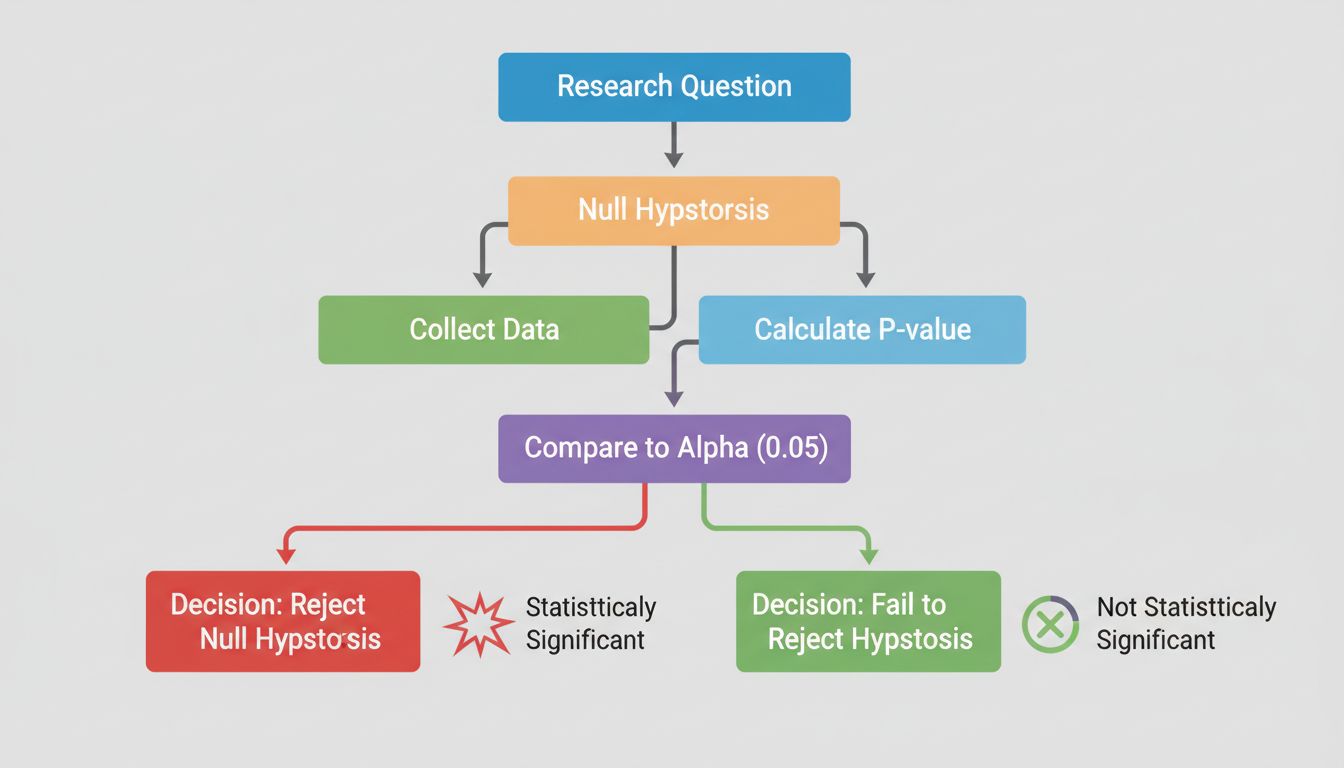
A statisztikai szignifikancia középpontjában a hipotézisvizsgálat áll, amely strukturált módszertan az adatokkal kapcsolatos állítások értékelésére. A folyamat két egymással versengő hipotézis megfogalmazásával kezdődik: a nullhipotézissel és az alternatív hipotézissel. A nullhipotézis azt feltételezi, hogy nincs valódi hatás vagy különbség a vizsgált csoportok között – lényegében ez a status quo, vagyis minden megfigyelt különbség pusztán véletlen eredménye. Ezzel szemben az alternatív hipotézis azt állítja, hogy valódi hatás vagy különbség létezik.
Vegyünk egy gyakorlati példát: teszteli, hogy egy új partner marketing kampány magasabb konverziós arányt eredményez-e, mint a jelenlegi megközelítés. A nullhipotézis szerint mindkét kampány azonos konverziós arányt produkál, míg az alternatív hipotézis szerint az új kampány eltérően teljesít. A statisztikai teszt ezután értékeli, melyik hipotézist támasztják alá jobban az adatok. Ez a keretrendszer megakadályozza, hogy a kutatók és elemzők csupán olyan eredményeket válasszanak ki, amelyek megerősítik várakozásaikat; ehelyett bizonyítaniuk kell, hogy az eredmények valószínűtlenek lennének pusztán a véletlen miatt.
A hipotézisvizsgálat szépsége az objektivitásában rejlik. Szubjektív megítélés helyett matematikai számításokat alkalmaz, hogy eldöntse, elegendő bizonyíték áll-e rendelkezésre a nullhipotézis elutasításához. Ha a bizonyíték elég erős, magabiztosan állíthatja, hogy a megfigyelt hatás statisztikailag szignifikáns – azaz valószínűtlen, hogy csak a véletlen műve.
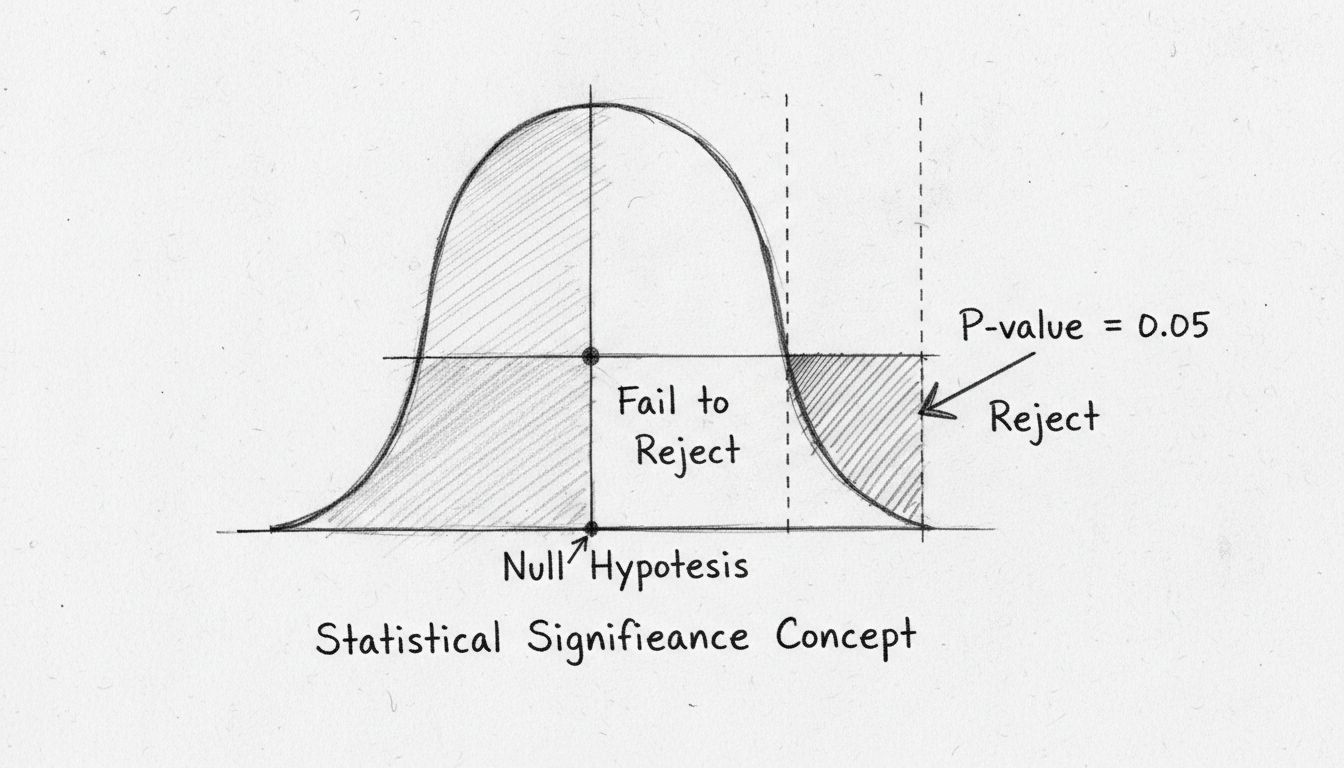
A p-érték talán a leggyakrabban használt, ám gyakran félreértett mérőszám a statisztikai szignifikancia vizsgálatában. A p-érték azt a valószínűséget mutatja meg, hogy a megfigyelt (vagy annál is szélsőségesebb) eredmények akkor is előfordulnának, ha a nullhipotézis igaz lenne. Másképp: „Mennyire valószínű, hogy ezt az adatot látnám, ha tényleg nem lenne hatás?” Az alacsony p-érték arra utal, hogy a megfigyelt eredmények nagyon valószínűtlenek a nullhipotézis mellett, vagyis valószínűleg hamis a nullhipotézis, és a hatás valós.
A statisztikai szignifikancia hagyományos küszöbértéke a 0,05-ös p-érték vagy kisebb, ami azt jelenti, hogy 5% az esélye annak, hogy az eredmények véletlenül fordultak elő. Ez azt jelzi, hogy elfogad egy 5%-os kockázatot a nullhipotézis helytelen elutasítására (I. típusú hiba). Ez a küszöbérték azonban némileg önkényes, és szakterülettől, kontextustól függően változik. Az orvosi kutatásban, ahol a téves pozitív eredmények súlyos következményekkel járhatnak, gyakran szigorúbb, például 0,01-es (1%) küszöböt alkalmaznak. Ezzel szemben feltáró jellegű vagy korai teszteléseknél a 0,10-es (10%) küszöb is elfogadható lehet.
| P-érték tartomány | Értelmezés | Tipikus teendő |
|---|---|---|
| p < 0,01 | Nagyon szignifikáns | Erős bizonyíték a nullhipotézis ellen |
| 0,01 ≤ p < 0,05 | Szignifikáns | Mérsékelt bizonyíték a nullhipotézis ellen |
| 0,05 ≤ p < 0,10 | Határeset szignifikáns | Gyenge bizonyíték a nullhipotézis ellen |
| p ≥ 0,10 | Nem szignifikáns | Nincs elegendő bizonyíték a nullhipotézis elutasításához |
Fontos megérteni, mit nem jelent a p-érték. Egy 0,03-as p-érték nem azt jelenti, hogy 97% az esélye annak, hogy a hipotézise igaz. Nem méri továbbá a hatás nagyságát vagy gyakorlati jelentőségét sem. Egy statisztikailag szignifikáns eredmény akár elhanyagolhatóan kis hatást is képviselhet, amelynek nincs valódi jelentősége. Ez a különbség a statisztikai és a gyakorlati szignifikancia között az egyik leggyakoribb félreértés az adatelemzésben.
Míg a p-értékek azt mutatják meg, hogy létezik-e hatás, a konfidencia-intervallumok kulcsfontosságú információt adnak a hatás mértékéről és pontosságáról. A konfidencia-intervallum egy olyan értéktartomány, amely nagy valószínűséggel tartalmazza a valódi hatásnagyságot, általában 95%-os megbízhatósági szinttel számolva. Ha például azt vizsgálja, hogy egy új partnerségi program funkció növeli-e a jutalékokat, egy 95%-os konfidencia-intervallum azt mutathatja, hogy a valódi növekedés 2% és 8% között van, 95%-os bizonyossággal.
A konfidencia-intervallumok számos előnnyel járnak a puszta p-értékekhez képest. Egyrészt közlik a hatás irányát és nagyságát, így teljesebb képet adnak az eredményekről. Másrészt segítenek a gyakorlati jelentőség megítélésében – ha egy hatás statisztikailag szignifikáns, de a konfidencia-intervallum szerint elhanyagolhatóan kicsi, lehet, hogy nem érdemes bevezetni. Harmadrészt, a szűk konfidencia-intervallumok pontos becslést, a szélesek pedig nagyobb bizonytalanságot jeleznek.
A hatásnagyság azt méri, hogy milyen erős a kapcsolat a változók között, illetve mekkora a különbség a csoportok között. Gyakori hatásnagyság-mutatók például a Cohen-féle d (átlagok összehasonlításához), a korrelációs együtthatók és az esélyhányadosok. Egy hatás lehet statisztikailag szignifikáns, de kis hatásnagyságú, vagyis gyakorlati jelentősége minimális. Ugyanakkor egy nagy hatásnagyságú eredmény nem biztos, hogy eléri a statisztikai szignifikanciát, ha a mintanagyság túl kicsi. A profi elemzők mindig a p-értékek mellett a hatásnagyságot is közlik, hogy teljes képet adjanak az eredményekről.
A mintanagyság alapvető szerepet játszik a statisztikai szignifikancia meghatározásában. A nagyobb minták több információt szolgáltatnak a populációról, csökkentik a véletlen ingadozás hatását, és könnyebbé teszik a valódi hatások kimutatását. Ezzel szemben a kis minták érzékenyebbek a véletlen ingadozásra, ami téves pozitív (nem létező hatás detektálása) vagy negatív (létező hatás elszalasztása) eredményekhez vezethet.
A mintanagyság és a statisztikai erő között szoros összefüggés van. A statisztikai erő annak valószínűsége, hogy a nullhipotézis hamissága esetén helyesen elutasítjuk azt – vagyis a valódi hatás felismerésének valószínűsége. A legtöbb kutató 0,80-as (80%-os) erőre törekszik, ami azt jelenti, hogy elfogad egy 20%-os esélyt arra, hogy elszalaszt egy valódi hatást. Ennek eléréséhez elegendően nagy mintára van szükség, amely a várt hatásnagyságtól, a választott szignifikanciaszinttől és a statisztikai teszt típusától függ.
Minden tanulmány vagy kísérlet előtt erőanalízist kell végezni a szükséges mintanagyság meghatározásához. Ez megakadályozza, hogy túl kicsi mintán dolgozzon, amely nem képes kimutatni a jelentős hatásokat, illetve elkerüli a túl nagy, idő- és költségigényes kutatásokat is. A partnerségi marketingben ez azt jelenti, hogy meg kell határozni, hány konverziót vagy kattintást kell megfigyelni ahhoz, hogy magabiztosan kijelenthesse: egy kampányváltozásnak valódi hatása van.
Különböző kutatási kérdésekhez és adattípusokhoz eltérő statisztikai tesztek szükségesek. A teszt kiválasztása függ például az összehasonlítandó csoportok számától, az adatok eloszlásától, a minták függetlenségétől vagy páros voltától, valamint az eredményváltozó típusától (folytonos, kategóriális stb.).
A Student-féle t-teszt két csoport átlagának összehasonlítására szolgál, és az egyik leggyakrabban használt teszt. Akkor alkalmazható, ha folytonos adatai vannak (pl. bevétel), és azt vizsgálja, eltérnek-e jelentősen a csoportok. A teszt figyelembe veszi a csoporton belüli szórást és a mintanagyságot, egy t-statisztikát adva, amelyet egy kritikus értékhez hasonlítanak a szignifikancia eldöntéséhez.
A khi-négyzet próba kategóriális adatoknál használatos annak meghatározására, hogy a megfigyelt gyakoriságok jelentősen eltérnek-e a várt értékektől. Ha például azt elemzi, hogy a partnercsatorna (e-mail, közösségi média, display hirdetés) befolyásolja-e a konverziós arányokat, a khi-négyzet teszt a megfelelő választás.
Az ANOVA (varianciaanalízis) a t-tesztet bővíti ki három vagy több csoport átlagának összehasonlítására. Ez megelőzi a többszörös összehasonlítás problémáját, amely során sok külön teszt végzése növelné a téves pozitív eredmények valószínűségét.
A Mann-Whitney U-teszt és a Wilcoxon rangösszeg teszt nemparaméteres alternatívák, amelyeket akkor alkalmaznak, ha az adatok nem felelnek meg a paraméteres tesztek feltételeinek, például nem normális eloszlásúak.
Az üzleti életben a statisztikai szignifikancia alapvető szerepet tölt be a döntéshozatalban számos területen. A marketingcsapatok A/B tesztelést alkalmaznak statisztikai szignifikanciával annak eldöntésére, hogy weboldal-módosítások, e-mail tárgysorok vagy hirdetési kreatívok valóban javítják-e a teljesítménymutatókat. A megérzésekre vagy kis mintákon szerzett tapasztalatokra alapozás helyett az adatvezérelt cégek előre meghatározzák a szignifikancia-küszöböket a tesztek előtt, így megbízható bizonyítékok alapján döntenek.
Kifejezetten a partnerségi marketingben a statisztikai szignifikancia segít azonosítani, mely partnerek, kampányok és promóciós stratégiák hoznak valóban bevételt, szemben azokkal, amelyek csak a véletlennek köszönhetően tűnnek sikeresnek. Ha például azt értékeli, hogy egy új jutalékszerkezet növeli-e a partnerek teljesítményét, a statisztikai tesztelés megóvja attól, hogy drága változtatásokat hajtson végre rövid távú ingadozások alapján. A PostAffiliatePro fejlett analitikai platformja lehetővé teszi, hogy partnermutatóit a szükséges statisztikai alapossággal kövesse nyomon, és magabiztos optimalizációs döntéseket hozzon.
A gyógyszeripari és orvosi kutatásokban a statisztikai szignifikancia dönti el, hogy az új kezelések elég hatékonyak-e az engedélyezéshez és alkalmazáshoz. A klinikai vizsgálatoknak bizonyítaniuk kell, hogy egy gyógyszer előnyei statisztikailag szignifikánsak, mielőtt a páciensek számára felírhatók lennének. A tét nagy, ezért az orvosi kutatásban általában szigorúbb szignifikancia szinteket alkalmaznak, mint más területeken.
Az egyik legelterjedtebb tévhit, hogy a statisztikai szignifikancia bizonyítja az oksági kapcsolatot. Egy statisztikailag szignifikáns korreláció két változó között nem jelenti azt, hogy az egyik okozza a másikat. A klasszikus példa a Nicolas Cage-filmek megjelenései és az úszómedence fulladásos balesetek közötti erős korreláció – nyilvánvaló, hogy egyik sem okozza a másikat. A statisztikai szignifikancia csak azt mutatja, hogy a kapcsolat valószínűtlenül véletlenszerű; az okság megállapításához további bizonyíték, például logikai kapcsolat, időbeli sorrend és kontrollált kísérletek szükségesek.
Egy másik gyakori hiba a p-hacking vagy adatbányászat, amikor a kutatók ugyanazon adathalmazon számos statisztikai tesztet végeznek, amíg szignifikáns eredményt nem találnak. Ez mesterségesen növeli a téves pozitív eredmények esélyét, hiszen elegendő teszt elvégzése után szinte biztos, hogy a véletlennek köszönhetően is talál szignifikáns eredményt. Ha például 20 független tesztet végez 0,05-ös szignifikancia szinten, várhatóan egy hamis pozitív eredmény pusztán a véletlen miatt is lesz. A felelős kutatók előre meghatározzák hipotéziseiket és a statisztikai teszteket az adatok elemzése előtt, elkerülve ezt a problémát.
A nem szignifikáns eredmények félreértelmezése is gyakori csapda. Egy nem szignifikáns eredmény nem bizonyítja, hogy nincs hatás; csupán azt jelenti, hogy nincs elegendő bizonyíték a nullhipotézis elutasításához. Ennek oka lehet a kis mintanagyság, nagy variabilitás az adatokban, vagy valóban hiányzó hatás. A bizonyíték hiánya nem azonos a hatás hiányának bizonyítékával.
A statisztika tudománya folyamatosan fejlődik, és egyre többen ismerik fel a hagyományos, p-érték-alapú megközelítések korlátait. Sok statisztikus ma már árnyaltabb megközelítést javasol, amely ötvözi a p-értékeket a hatásnagysággal, konfidencia-intervallumokkal és Bayes-féle módszerekkel. A Bayes-statisztika, amely a korábbi tudást beépíti, és a megfigyelt adatok alapján frissíti a hiedelmeket, alternatív keretet ad, amelyet néhány kutató intuitívabbnak és rugalmasabbnak tart a gyakorisági megközelítésnél.
A szekvenciális tesztelés és az adaptív kísérlettervezés egyre népszerűbb, lehetővé téve, hogy a kutatók az adatok beérkezésével nyomon kövessék az eredményeket, és menet közben döntsenek a kísérlet folytatásáról, módosításáról vagy leállításáról. Ez különösen értékes az üzleti életben, ahol a döntéseket gyorsan kell meghozni. Az olyan eszközök, mint a Statsig Stats Engine szekvenciális tesztelést valósítanak meg hamis felfedezési ráta kontrollal, gyorsabb és pontosabb döntéshozatalt lehetővé téve a kísérletek során.
A tudományos replikációs válság is rámutatott a statisztikai szignifikancia helyes értelmezésének fontosságára. Sok publikált eredmény nem reprodukálható, részben azért, mert a kutatók és folyóiratok túlzottan a statisztikai szignifikancia elérésére koncentráltak, miközben figyelmen kívül hagyták a hatásnagyságot és a gyakorlati jelentőséget. A jövőben a hangsúly egyre inkább az átláthatóságra, a tanulmányok előzetes regisztrációjára és az összes eredmény közlésére tolódik – függetlenül attól, hogy szignifikánsak-e vagy sem.
A statisztikai szignifikancia hatékony használatához a vizsgálat előtt határozza meg a szignifikanciaszintet és a szükséges mintanagyságot. Ez megakadályozza, hogy az eredmények ismeretében módosítsa a küszöböket. Mindig közölje a hatásnagyságot és a konfidencia-intervallumot a p-érték mellett, hogy teljes képet adjon az eredményekről. Vegye figyelembe az eredmények gyakorlati jelentőségét is – egy statisztikailag szignifikáns hatás lehet, hogy túl kicsi ahhoz, hogy valódi üzleti alkalmazást indokoljon.
Legyen átlátható a módszertanában, beleértve azt is, hogyan kezelte a hiányzó adatokat, kiugró értékeket és többszörös tesztelést. Ha több tesztet végzett, alkalmazzon megfelelő korrekciókat, például Bonferroni korrekciót a teljes szignifikanciaszint fenntartásához. Dokumentálja az elemzési folyamatot, és legyen kész megosztani adatait és kódját másokkal az ellenőrzés és reprodukálhatóság érdekében.
Végül ne feledje, hogy a statisztikai szignifikancia eszköz, nem végcél. Segíti a jobb döntéshozatalt azáltal, hogy csökkenti a véletlen szerepét, de csak szakmai ismeretekkel, gyakorlati megfontolásokkal és üzleti ítélőképességgel együtt alkalmazva hoz valóban jó döntéseket. A partnerségi marketingben a statisztikai szignifikancia segít felismerni, mely stratégiák javítják valóban a teljesítményt, de a stratégiai döntéseknél érdemes figyelembe venni az implementációs költségeket, a partnerek elégedettségét és a hosszú távú fenntarthatóságot is.
A PostAffiliatePro fejlett analitikai és jelentéskészítő eszközei segítenek statisztikai alapossággal nyomon követni a partnerek teljesítményét. Ismerje meg, mely kampányok hoznak valóban eredményeket, és optimalizálja partnerprogramját megbízható adatelemzések alapján.

Fedezze fel, miért számít a statisztikai szignifikancia az adatelemzésben, a kutatásban és az üzleti döntésekben. Ismerje meg a p-értékeket, a hipotézisvizsgála...
A statisztikai szignifikancia a mért adatok megbízhatóságát fejezi ki, segítve a vállalkozásokat abban, hogy megkülönböztessék a valódi hatásokat a véletlentől,...
Sajátítsa el a statisztikai szignifikancia fogalmát az A/B tesztelésben a fogadási partner kampányokhoz. Ismerje meg a p-értékeket, konfidenciaszinteket....
Sütik Hozzájárulás
A sütiket használjuk, hogy javítsuk a böngészési élményt és elemezzük a forgalmunkat. See our privacy policy.